第8回　順番を確定させずに協力する――プロセスマトリクスという構成

量子力学では、操作の順序が結果に影響することがある。測定してから操作する場合と、操作してから測定する場合とでは、得られる結果が異なることがある。これは一見すると当たり前の話に見えるかもしれないが、量子系ではこうした順序の影響が非常に本質的な意味を持つ。

では、そもそも操作の順番そのものが定まっていない――そんな構成は成り立つだろうか？

プロセスマトリクスという理論は、順序が未定義な構成を量子力学の枠内できちんと記述するための枠組みとして提案された。今回は、その理論が立ち上がる背景にある「順序による制約」と、その限界を超えるための構成について見ていこう。

Quantum correlations with no causal order | Nature Communications より

協力ゲームと古典的な限界

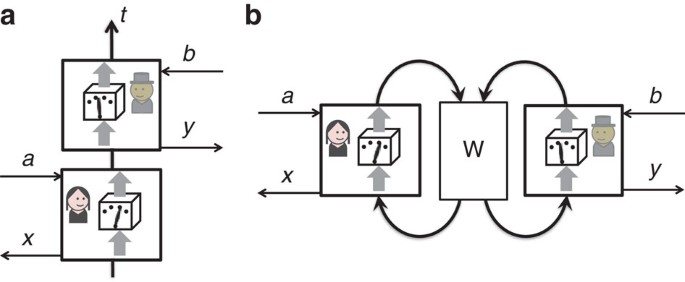
まず、量子力学とは無関係な構成から出発する。AとBという二人が参加する、簡単な協力型のゲームを考えよう。ゲームは次のように進む：

AとBは、それぞれ1ビットのランダムな入力（a, b）を受け取る
それぞれが1ビットの出力（x, y）を返す
操作の順番は毎回ランダムに決まり、「Aが先」「Bが先」のどちらかになる
先に操作する側の出力は、後の側に渡される

評価者は、Bの出力 y が A の入力 a に一致しているか（y = a）だけを見て成功かどうかを判断する。ただし、その回でどちらが先だったかという順序は評価者には知らされない。

このルールの下では、操作の順序によって成功率が変わる。A→Bの順序ならBはAの出力を参照できるので、成功率は1になる。B→Aの順序ではBはaを知らないので、成功率は0.5が限界となる。順序は毎回ランダムなので、成功率の平均は最大でも0.75にとどまる。これが、古典的構成で達成可能な限界だ。

順序を確定させずに相関を強める

この古典的限界を超えるにはどうすればいいか。プロセスマトリクス理論は、その問いに対する量子的なアプローチだ。

この理論では、順序を「Aが先」「Bが先」といったどちらかに決めるのではなく、そもそも順序が定義されていないという構成を考える。どういうことかというと、Aの操作がBの結果に影響を与え、同時にBの操作がAの結果に影響を与えているにもかかわらず、そのどちらが先だったのかをどの観測記録からも確定できないという状況が成り立つ。このとき、操作の順序が「重ね合わされた状態」にあるとも表現される。

このような順序未定義な構成では、情報をやり取りしたような相関が実現するのに、それが観測記録として残らない。干渉が壊れずに維持される。この条件のもとでは、成功率が0.75を超えて0.85近くに達する構成が理論上可能になる。これは、古典的な構成では決して実現できない相関だ。

「それって情報を渡してるだけでは？」という疑問

ここで多くの人が疑問に思うはずだ。「結局、情報が行き来してるんじゃないの？　だったら、むしろ成功率は1になるべきじゃないのか？」

これは非常にもっともな疑問だ。古典的な構成では、Aの入力aがBに確実に渡れば、Bはそれを出力できる。成功率は1になる。ところがプロセスマトリクスでは、理論的に0.85が限界とされている。ということは、情報が「使われている」ように見えても、それには何らかの制約がかかっているということになる。

決定的なのは、「干渉を維持する」という条件だ。この理論では、AとBの操作のあいだにどちらが先だったかという順序を、外部の観測者が特定できてはならない。もし順序が明確にわかってしまえば、量子的な干渉は壊れてしまう。プロセスマトリクスが前提としている構成が崩れる。

たとえば、BがAの入力aを確実に取得してそれを出力した場合、観測者はその一致を見て「BはAの情報を受け取った」と推測できてしまう。そうなると、「B→A」の順序ではありえないということになり、順序が事実上確定してしまう。順序を確定させずに干渉を維持することが目標である以上、そのような構成は除外される。

つまり、プロセスマトリクスの枠内では「完全な情報伝達」は許されていない。相関を強くすることと、干渉を維持することのあいだにはトレードオフがあり、その限界の中で最大限成功率を高めた結果が0.85という値なのだ。

このような構成では、AとBがそれぞれ自分の手元の入力と量子的な背景を利用しながら、あたかも通信しているかのような相関を作り出している。しかしそれは、古典的な意味での「通信」とは違う。通信であれば情報の痕跡が観測記録として残るはずだが、ここではそのような痕跡は存在しない。順序は確定しておらず、干渉は壊れていない。だからこそ、これは古典的制約を超えた量子的相関として意味を持つ。

プロセスマトリクス理論は、こうした制約の中でどこまで相関を構成できるかを探る枠組みであり、量子力学が持つ因果構造の限界を問う試みでもある。

因果の境界としての構成と、実験との接点

「因果律が壊れている」という言い方は正しいか？

プロセスマトリクス理論に対しては、「因果律が壊れている」や「時間が消えた」といった表現が使われることがある。だが、今回扱った協力ゲームの構成を見れば、そのような言い方が正確でないことは明らかだ。

ここで私たちは、順序を確定させないように構成することで干渉を保ち、相関を最大化するという仕組みを見た。つまり、順序を「壊している」わけではなく、「壊さずに曖昧に保っている」ことが重要だった。順序を確定させてしまうと因果的整合性が崩れるのではなく、逆に構成そのものが破綻してしまう。

この構成では、因果関係の破綻が許容されているのではなく、順序に依存しない形での因果的一貫性が求められている。だからこそ、「因果律が壊れている」という表現はこの文脈には当てはまらない。プロセスマトリクス理論は、因果の不在ではなく、因果の構成の自由度と制約のバランスを問う理論なのだ。

実験との接点はどこまであるか？

こうした構成は、理論上では成功率0.85に達することが可能だとされているが、現実の量子実験でこの数値に匹敵する結果が得られたわけではない。ただし、順序を明確に定めない構成を実際に光子系で設計し、干渉を保ったまま操作を施すといった試みはすでに始まっている。たとえばQuantum Switchと呼ばれる構成を用いた実験では、順序が未定義な状況でも干渉が維持されていることが確認されている。

今回扱った協力ゲーム型の構成とは異なるが、順序が未定義なまま操作が行われるという特徴を部分的に共有しているという点で、理論の可能性が現実に接近しつつあることは確かだ。ただし、構成全体がそのまま実現されたわけではなく、成功率に関する数値も理論的な水準には至っていない。