素因数分解は、一見すると単純な問題に見える。ある自然数 $N$ を、どの素数の積で表せるかを調べるだけだ。だが、この単純さの裏には、計算上の深い難しさがある。特に $N$ が非常に大きくなったとき、効率よく因数を求める手段は限られている。
Shor のアルゴリズムが与えたのは、因数の探し方ではなかった。素因数分解という問題そのものを、まったく異なる構造をもった別の問題へと変形するという視点だった。その構造とは、「周期性をもつ関数をつくる」ことである。
この回では、Shor のアルゴリズムの核心である「周期を見つける」という構造をどう物理的に準備するか、すなわち、周期をもつ構造を量子状態としてどうやって作るかに焦点を当てる。周期から因数を得る工程や、観測の仕方については次回に扱う。
周期性をもつ関数 $f(x) = a^x \bmod N$
まず、素因数分解したい自然数 $N$ に対して、$1 < a < N$ の範囲から $N$ と互いに素な整数 $a$ を選び、次の関数を考える:
$$
f(x) = a^x \bmod N
$$
この関数は、ある正の整数 $r$ を周期として、
$$
f(x) = f(x + r)
$$
がすべての整数 $x$ に対して成り立つような性質をもっている。周期 $r$ が存在するということは、$f(x)$ の値の並びが $r$ ごとに正確に繰り返されるという意味であり、途中で別の値が混ざったり、周期から外れた一致が起こったりすることはない。
このように、$f(x) = a^x \bmod N$ の周期 $r$ を見つけることで因数分解に結びつける構造は、「位数に基づく因数分解法」と呼ばれており、量子計算とは無関係に古くから知られている。
Shor のアルゴリズムが新たに与えたのは、この周期 $r$ を量子的な構成によって一括で抽出できるようにするという視点だった。だがまずは、その周期構造をどうやって物理的に作るのかを考える必要がある。
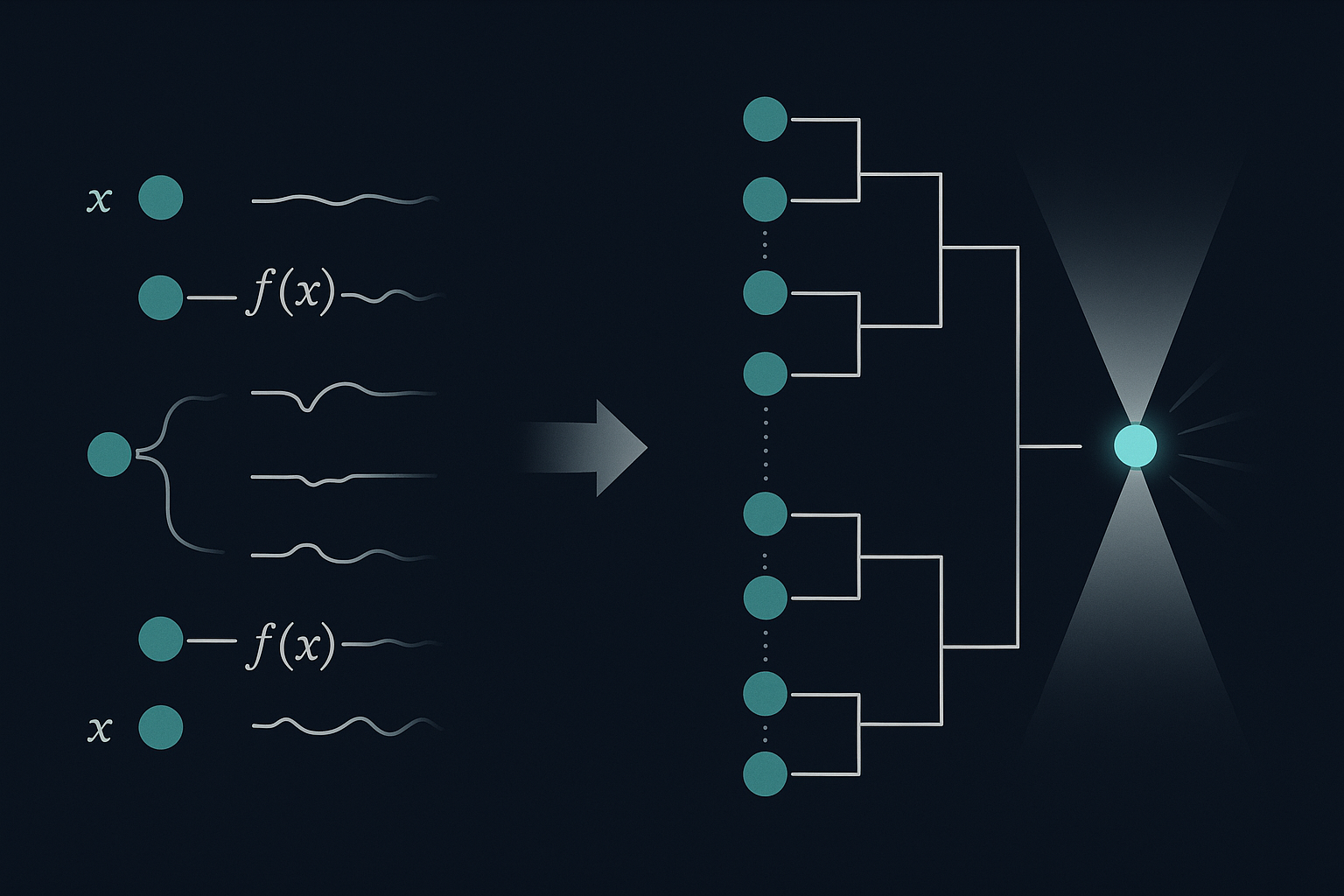
量子回路では、周期を含んだ構造をまとめて作ることができる
Shor の量子構成では、まず複数の量子ビットを使って、整数 $x = 0$ から $Q – 1$ までの値を重ね合わせた状態を作る。ここで $Q$ は、周期を後に十分な精度で抽出できるよう、$N^2$ より大きい 2 のべき乗として選ばれる。
この重ね合わせ状態は、各ビットに Hadamard ゲートを一度ずつかけることで実現される。$x = 0$ から $Q – 1$ までの全ての $x$ を等重みに含んだ重ね合わせが、一括で得られる。
次に、この $x$ に対応する $f(x) = a^x \bmod N$ を別の量子ビット列に書き込む操作を行う。ここで必要になるのが、$f(x)$ を計算するためのユニタリな量子回路である。
この回路は、次のような段階を経て構成される:
- 累乗 $a^x$ の構成:
$x$ をビット列 $x = x_0 + 2x_1 + 4x_2 + \dots$ と見て、それぞれの $x_i$ に応じて $a^{2^i}$ を掛けるかどうかを制御する操作を並べる。これは制御された乗算で構成される。 - 乗算の構成:
量子回路上での乗算は、加算回路を繰り返す構造で実装され、$n$ ビットの整数同士の乗算であれば $O(n^2)$ の回路で可能になる。 - 剰余演算 $\bmod N$ の実装:
演算結果が $N$ を超えるかどうかを量子的に比較し、必要に応じて $N$ を引く操作を加える。この比較や減算もユニタリに構成でき、必要な回路規模は乗算と同程度になる。 - 逆演算の導入:
中間変数を消去し、ユニタリ性を保つためにアンコンピュート操作を加える。
これらを組み合わせることで、$f(x) = a^x \mod N$ を一括で計算する量子回路が構成される。その規模はビット長 $n = \log N$ に対して $O(n^3)$ 程度で収まる。
古典的に $f(x)$ を1つずつ計算して周期を探そうとする場合、$x$ の候補は最大で $N$ 個程度必要になる。そのため全体の計算量は $O(N)$ に比例して増大し、指数的な増加を避けられない。一方、量子回路では回路一つを構成すれば、重ね合わせに含まれるすべての $x$ に対して $f(x)$ を同時に書き込むことができる。計算量としても構造としても、古典と量子の違いは明確に現れる。
このようにして得られる変換:
$$
|x\rangle |0\rangle \mapsto |x\rangle |f(x)\rangle
$$
は、すべての $x$ に対して同時に実行される。これは、並列コンピュータのように複数のプロセッサを並べて個別に計算しているのではなく、一つの量子回路が重ね合わせ全体に一括して作用するという構造を持っている。物理的に必要なのは、あくまでその $f(x)$ を計算するユニタリな回路一つであり、その回路がすべての $x$ に並列に作用している。
構成された状態の中には、周期構造が明確に存在している
このようにして得られた状態では、出力側の $f(x)$ の値が同じであるような $x$ の集合──すなわち $x, x+r, x+2r, \dots$ のような系列──が、同じ出力状態 $|f(x)\rangle$ に対応する形でまとめられる。入力状態は、周期 $r$ ごとの構造を保った重ね合わせになっており、周期性が量子状態の中に物理的に組み込まれている。
つまり、周期性は関数の性質としてではなく、構成された状態として物理的に現れている。これが、Shor のアルゴリズムにおける構成上の本質である。
この状態をそのまま観測しても、周期が露出してくるわけではない。今作った構造はあくまで「干渉の素材」であり、周期を浮かび上がらせるにはさらに変換操作が必要となる。そのための準備として、重ね合わせの範囲を $Q > N^2$ に設定し、周期構造が明瞭に状態内に刻まれるようにしてある。
この回のまとめ:周期は見つけるのではなく、状態として作る
Shor のアルゴリズムは、周期 $r$ を持つ関数を使うというだけでなく、その周期性を量子状態の中に構成として作り込む。その工程によって、周期という構造が「探す対象」ではなく「物理的に作られた状態」として扱われるようになる。
この構成は、後の観測で周期を取り出せるように、干渉が起きる設計にもなっている。そのための準備段階として、$Q$ の選び方や回路の規模も含めて、周期構造を状態に刻む工程が Shor の最初の要所になる。
次回は、この構成された状態から周期を取り出すための操作──量子 Fourier 変換とその観測による抽出──について扱う。

コメント